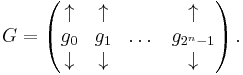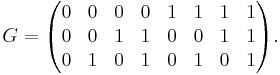Walsh–Hadamard code
In coding theory, the Walsh–Hadamard code, named after the American mathematician Joseph Leonard Walsh and the French mathematician Jacques Hadamard, is an example of a linear code over a binary alphabet that maps messages of length  to codewords of length
to codewords of length 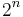 . The Walsh–Hadamard code is unique in that each non-zero codeword has Hamming weight of exactly
. The Walsh–Hadamard code is unique in that each non-zero codeword has Hamming weight of exactly 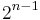 , which implies that the distance of the code is also
, which implies that the distance of the code is also 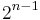 . In standard coding theory notation, this means that the Walsh–Hadamard code is a
. In standard coding theory notation, this means that the Walsh–Hadamard code is a ![[2^n,n,2^n/2]_2](/2012-wikipedia_en_all_nopic_01_2012/I/1651695bf210777e47876f8822fa10e9.png) -code. The Hadamard code can be seen as a slightly improved version of the Walsh–Hadamard code as it achieves the same block length and minimum distance with a message length of
-code. The Hadamard code can be seen as a slightly improved version of the Walsh–Hadamard code as it achieves the same block length and minimum distance with a message length of 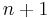 , that is, it can transmit one more bit of information per codeword, but this improvement comes at the expense of a slightly more complicated construction.
, that is, it can transmit one more bit of information per codeword, but this improvement comes at the expense of a slightly more complicated construction.
The Walsh–Hadamard code is a locally decodable code, which provides a way to recover parts of the original message with high probability, while only looking at a small fraction of the received word. This gives rise to applications in computational complexity theory and particularly in the design of probabilistically checkable proofs. It can also be shown that, using list decoding, the original message can be recovered as long as less than 1/2 of the bits in the received word have been corrupted.
In code division multiple access (CDMA) communication, the Walsh–Hadamard code is used to define individual communication channels. It is usual in the CDMA literature to refer to codewords as “codes”. Each user will use a different codeword, or “code”, to modulate their signal. Because Walsh–Hadamard codewords are mathematically orthogonal, a Walsh-encoded signal appears as random noise to a CDMA capable mobile terminal, unless that terminal uses the same codeword as the one used to encode the incoming signal.[1]
Contents |
Definition
The 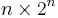 generator matrix
generator matrix  for the Walsh–Hadamard code of dimension
for the Walsh–Hadamard code of dimension  is given by
is given by
where  is the vector corresponding to the binary representation of
is the vector corresponding to the binary representation of  . In other words,
. In other words,  is the list of all vectors of
is the list of all vectors of 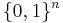 in some lexicographic order. For example, the generator matrix for the Walsh–Hadamard code of dimension 3 is
in some lexicographic order. For example, the generator matrix for the Walsh–Hadamard code of dimension 3 is
As is possible for any linear code generated by a generator matrix, we encode a message 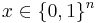 , viewed as a row vector, by computing its codeword
, viewed as a row vector, by computing its codeword 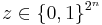 using the vector-matrix product in the vector space over the finite field
using the vector-matrix product in the vector space over the finite field  :
:
This way, the matrix  defines a linear operator
defines a linear operator  and we can write
and we can write 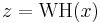 .[2]
.[2]
A more explicit, equivalent definition of  uses the scalar product
uses the scalar product  over
over  :
:
- For any two strings
 , we have
, we have 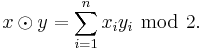
Then the Walsh–Hadamard code is the function  that maps every string
that maps every string 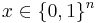 into the string
into the string 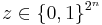 satisfying
satisfying  for every
for every  (where
(where  denotes the
denotes the  th coordinate of
th coordinate of  , identifying
, identifying 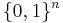 with
with 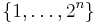 in some way).
in some way).
Distance
The distance of a code is the minimum Hamming distance between any two distinct codewords, i.e., the minimum number of positions at which two distinct codewords differ. Since the Walsh–Hadamard code is a linear code, the distance is equal to the minimum Hamming weight among all of its non-zero codewords. All non-zero codewords of the Walsh–Hadamard code have a Hamming weight of exactly 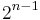 by the following argument.
by the following argument.
Let 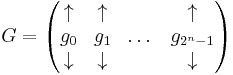 be the
be the 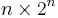 generator matrix for a Walsh-Hadamard code of dimension
generator matrix for a Walsh-Hadamard code of dimension  .
.
Let  represent the Hamming weight of vector
represent the Hamming weight of vector  .
.
Let 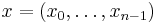 be a non-zero message in
be a non-zero message in 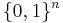 .
.
We want to show that 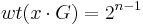 for all non-zero codewords. Remember that all arithmetic is done over
for all non-zero codewords. Remember that all arithmetic is done over 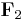 , which is the finite field of size 2.
, which is the finite field of size 2.
Let  be a non-zero bit of arbitrary message,
be a non-zero bit of arbitrary message,  . Pair up the columns of
. Pair up the columns of  such that for each pair
such that for each pair  ,
,  (where
(where 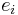 is the zero vector with a 1 in the
is the zero vector with a 1 in the 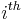 position). By the way
position). By the way  is constructed, there will be exactly
is constructed, there will be exactly 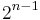 pairs. Then note that
pairs. Then note that 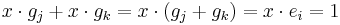 .
. 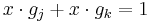 , implies that exactly one of
, implies that exactly one of 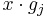 ,
,  must be 1. There are
must be 1. There are 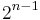 pairs, so
pairs, so  will have exactly
will have exactly 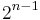 bits that are a 1.
bits that are a 1.
Therefore, the Hamming weight of every codeword in the code is exactly 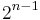 .
.
Being a linear code, this means that the distance of the Walsh-Hadamard code is 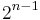 .
.
Locally Decodable
A locally decodable code is a code that allows a single bit of the original message to be recovered with high probability by only looking at a small portion of the received word. A code is  -query locally decodable if a message bit,
-query locally decodable if a message bit,  , can be recovered by checking
, can be recovered by checking  bits of the received word. More formally, a code,
bits of the received word. More formally, a code, 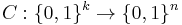 , is
, is  -locally decodable, if there exists a probabilistic decoder,
-locally decodable, if there exists a probabilistic decoder, 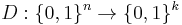 , such that (Note:
, such that (Note: 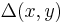 represents the Hamming distance between vectors
represents the Hamming distance between vectors  and
and  ):
):
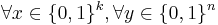 ,
, 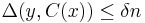 implies that
implies that ![Pr[D(y)_i = x_i] \geq \frac{1}{2} %2B \epsilon, \forall i \in [k]](/2012-wikipedia_en_all_nopic_01_2012/I/7326f23ed74f1f6eeab2e3eb921a3ce4.png)
Theorem 1: The Walsh–Hadamard code is  -locally decodable for
-locally decodable for 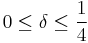 .
.
Lemma 1: For all codewords,  in a Walsh–Hadamard code,
in a Walsh–Hadamard code,  ,
, 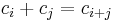 , where
, where 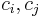 represent the bits in
represent the bits in  in positions
in positions  and
and  respectively, and
respectively, and 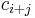 represents the bit at position
represents the bit at position  .
.
Proof of Lemma 1
Let 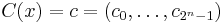 be the codeword in
be the codeword in  corresponding to message
corresponding to message 
Let 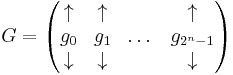 be the generator matrix of
be the generator matrix of 
By definition, 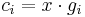 . From this,
. From this, 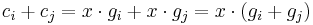 . By the construction of
. By the construction of  ,
, 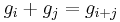 . Therefore, by substitution,
. Therefore, by substitution,  .
.
Proof of Theorem 1
To prove theorem 1 we will construct a decoding algorithm and prove its correctness.
Algorithm
Input: Received word 
For each 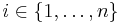 :
:
- Pick
 independently at random
independently at random - Pick
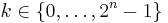 such that
such that 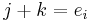 where
where  is the bitwise xor of
is the bitwise xor of  and
and  .
. 
Output: Message 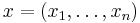
Proof of correctness
For any message,  , and received word
, and received word  such that
such that  differs from
differs from 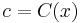 on at most
on at most 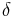 fraction of bits,
fraction of bits,  can be decoded with probability at least
can be decoded with probability at least 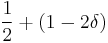 .
.
By lemma 1, 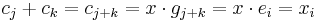 . Since
. Since  and
and  are picked uniformly, the probability that
are picked uniformly, the probability that 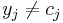 is at most
is at most 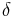 . Similarly, the probability that
. Similarly, the probability that  is at most
is at most 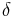 . By the union bound, the probability that either
. By the union bound, the probability that either 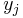 or
or 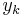 do not match the corresponding bits in
do not match the corresponding bits in  is at most
is at most  . If both
. If both 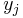 and
and 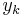 correspond to
correspond to  , then lemma 1 will apply, and therefore, the proper value of
, then lemma 1 will apply, and therefore, the proper value of  will be computed. Therefore the probability
will be computed. Therefore the probability  is decoded properly is at least
is decoded properly is at least 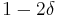 . Therefore,
. Therefore,  and for
and for  to be positive,
to be positive, 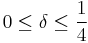 .
.
Therefore, the Walsh–Hadamard code is  locally decodable for
locally decodable for 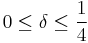
See also
Notes
- ^ "CDMA Tutorial: Intuitive Guide to Principles of Communications". Complex to Real. http://www.complextoreal.com/CDMA.pdf. Retrieved 4 August 2011.
- ^ Section 19.2.2 of Arora & Barak (2009).
References
- Arora, Sanjeev; Barak, Boaz (2009), Computational Complexity: A Modern Approach, Cambridge, ISBN 978-0-521-42426-4, http://www.cs.princeton.edu/theory/complexity/
- Lecture notes of Atri Rudra: Hamming code and Hamming bound